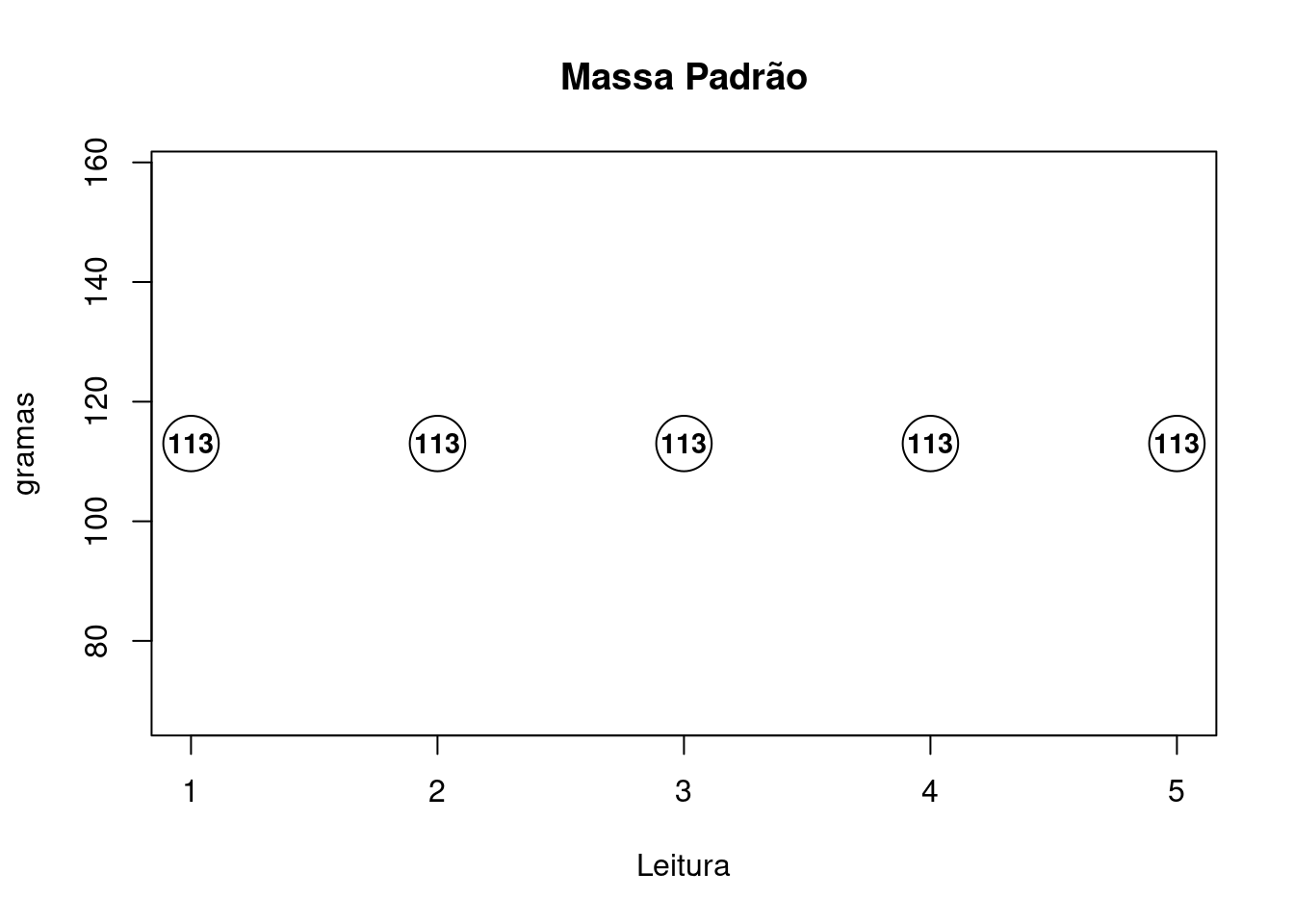
Procedimento 1: Calibração da Balança

Utilize a massa padrão para calibrar uma balança digital. A massa padrão possui valor nominal de \(140g\), incerteza de \(0.2g\), correção de \(+1g\) e \(4\) graus de liberdade.

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade A Normal Amostrado
Calibração da Massa Padrão B Normal \(\pm 2g\), \(v=4\)
Resolução da Balança B Uniforme \(1g\)
Correção da Massa Padrão - - \(+1g\)

values
\(U_{cal}\) 0.6970304
\(U_{rep}\) 0.0000000
\(U_{res}\) 0.2886751
\(U_c\) 0.7544433
\(\nu_{eff}\) 5.0000000
\(U_{exp}\) 1.9982596
\(C_c\) 2.0000000
1 Algarismo Significativo 2 Algarismos Significativos
Cb = ( 2 \(\pm\) 2 ) \(g\) com 95.45 % de confiança Cb = ( 2.0 \(\pm\) 2.0 ) \(g\) com 95.45 % de confiança

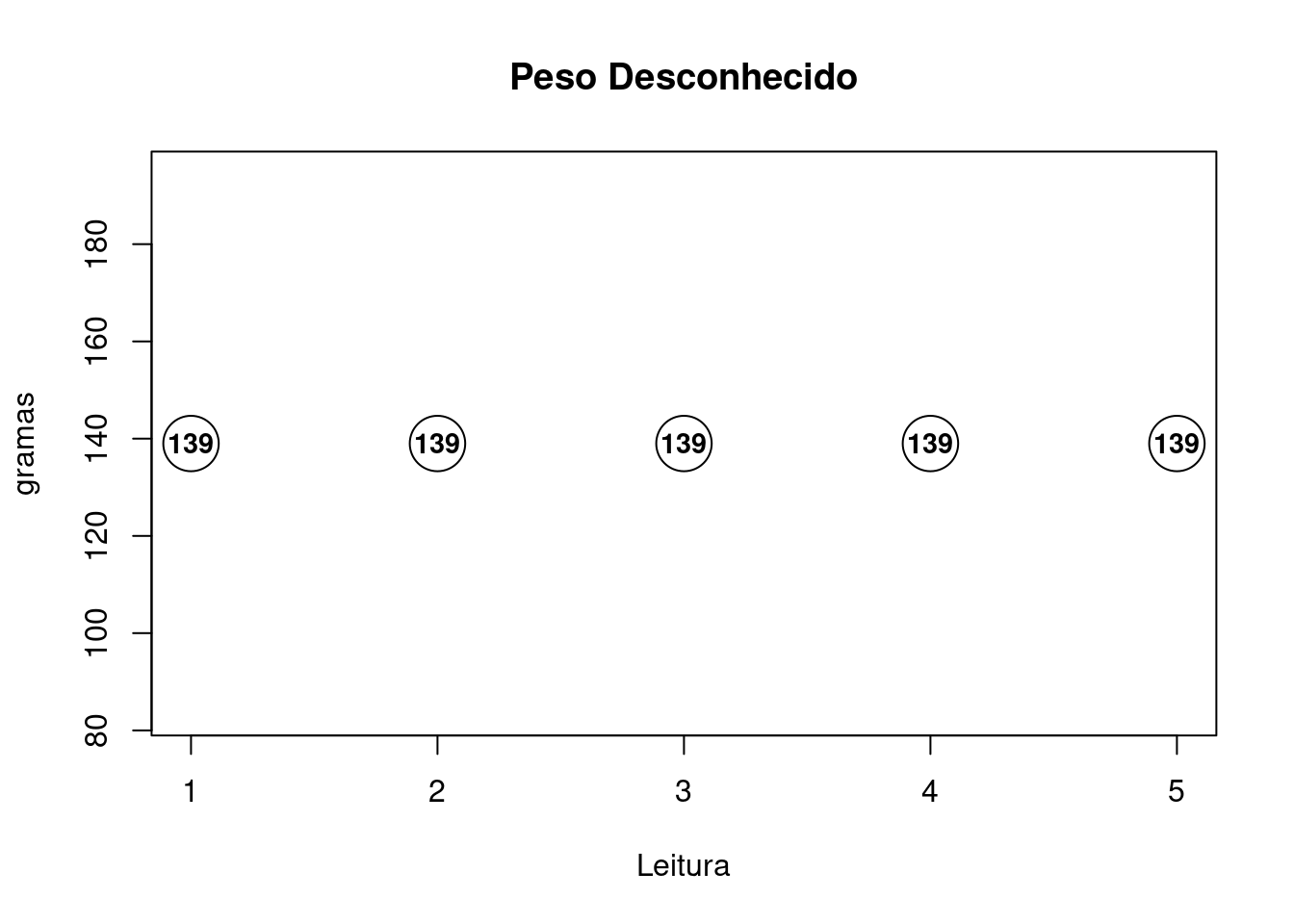
Procedimento 2: Calibração da Massa Desconhecida

Uma vez calibrada a balança identifique a massa de um objeto. Sobre a balança conhecemos somente as informações de correção, incerteza e graus de liberdade resultantes do procedimento anterior.

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade A Normal Amostrado
Calibração da Balança B Normal ver Procedimento 1
Resolução da Balança B Uniforme \(1g\)

values
\(U_{cal}\) 0.7544433
\(U_{rep}\) 0.0000000
\(U_{res}\) 0.2886751
\(U_c\) 0.8077859
\(\nu_{eff}\) 6.5712591
\(U_{exp}\) 1.9891858
\(\bar{M}+C_c\) 141.0000000
1 Algarismo Significativo 2 Algarismos Significativos
RM = ( 141 \(\pm\) 2 ) \(g\) com 95.45 % de confiança RM = ( 141.0 \(\pm\) 2.0 ) \(g\) com 95.45 % de confiança

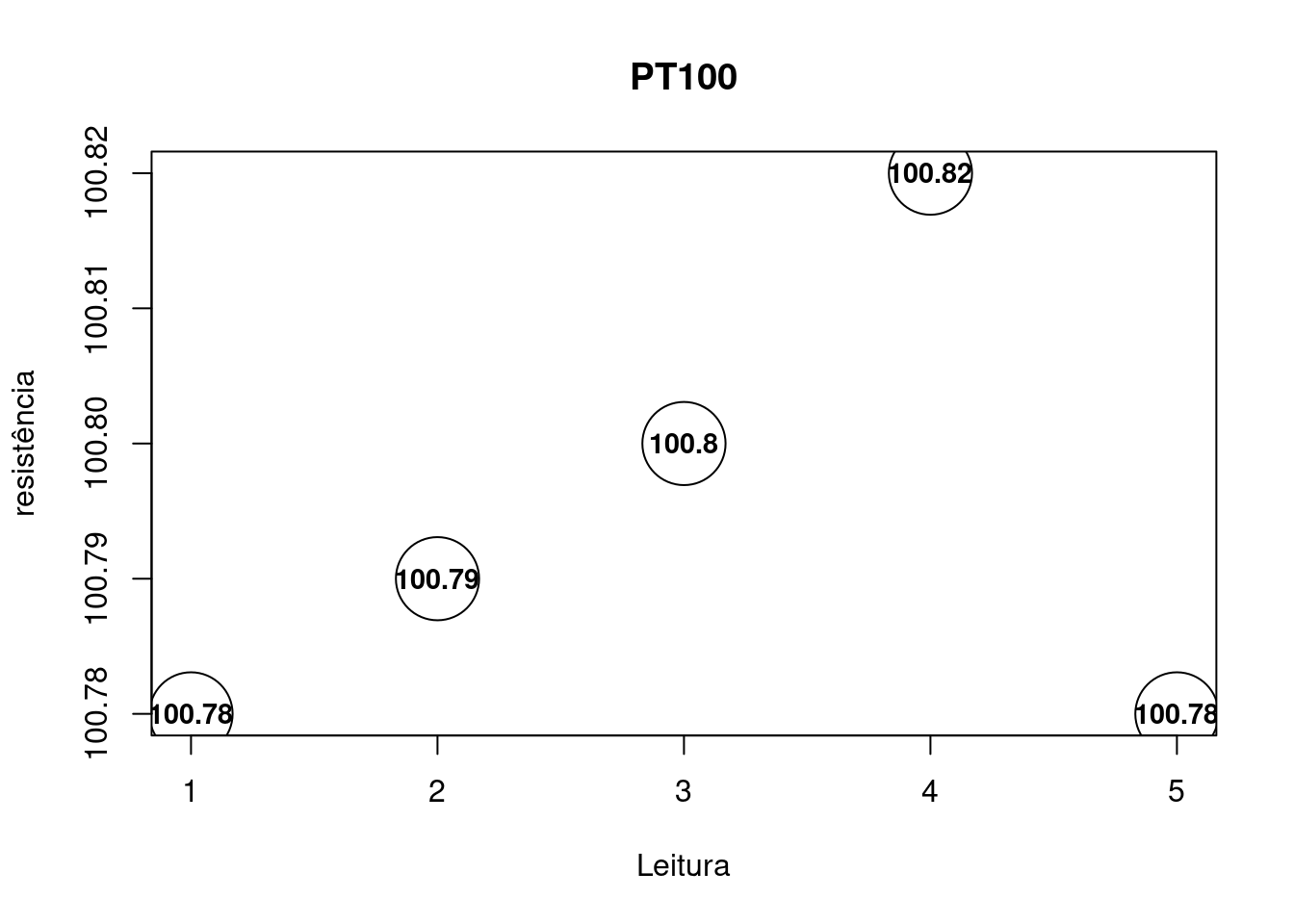
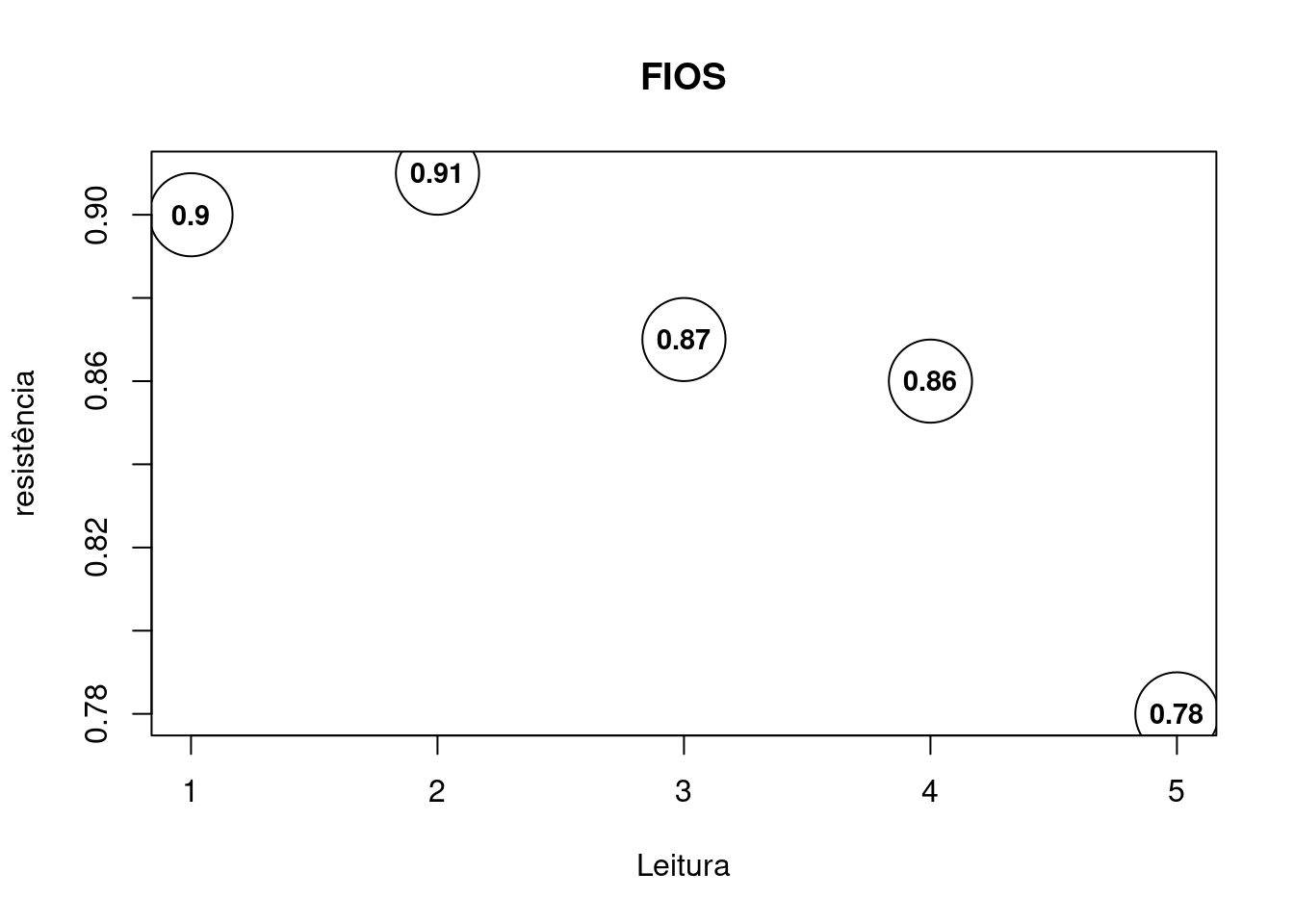
Procedimento 3: Calibração PT100 (Resistências)

Com o sensor PT100 em \(0^oC\) (forno calibrado) identifique a resistência do sensor levando em consideração as incertezas do calibrador CA71. Faça medições da resistência de modo que \(R=R_{PT100}-R_{FIOS}\).

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade \(R_{PT100}\) A Normal Amostrado
Repetitividade \(R_{FIOS}\) A Normal Amostrado
Calibração do CA71 B Normal \(\pm (0.05\%+0.1\Omega)\) para \((23\pm5)^oC\)
Resolução do CA71 B Uniforme \(0.01\Omega\)
Temperatura do CA71 B Normal \(Calibração*(1/5)/^oC\)

Outras informações:

values
\(U_{cal-PT100}\) 0.0751985
\(U_{cal-FIOS}\) 0.0502160
\(U_{rep-PT100}\) 0.0074833
\(U_{rep-FIOS}\) 0.0229347
\(U_{res}\) 0.0028868
\(U_{temp-PT100}\) 0.0240635
\(U_{temp-FIOS}\) 0.0160691
\(U_c\) 0.0980428
\(\nu_{eff}\) 1320.0000000
\(U_{exp}\) 0.1962718
1 Algarismo Significativo 2 Algarismos Significativos
RM = 99.9 \(\pm\) 0.2 \(^oC\) com 95.45 % de confiança RM = 99.93 \(\pm\) 0.20 \(^oC\) com 95.45 % de confiança

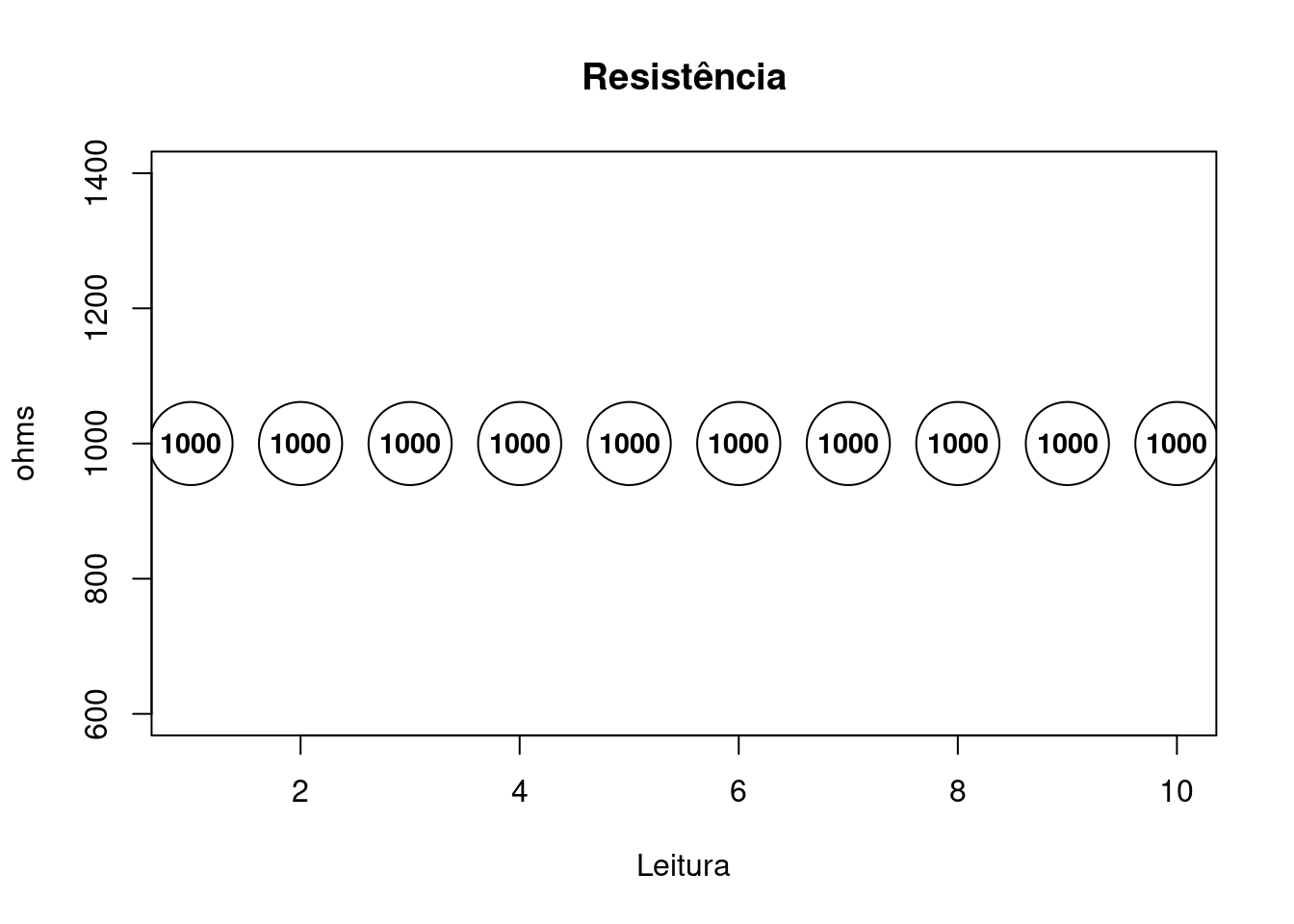
Procedimento 4: Ohmímetro

Calibre o ohmímetro utilizando como referência a década resistiva.

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade A Normal Amostrado
Calibração da Década B Normal \(\pm(0.01\%+2m\Omega)\) para \((23\pm2)^oC\)
Resolução da Década B Uniforme \(0.001\Omega\)
Resolução do Multímetro B Uniforme \(1\Omega\) (na escala de \(2k\Omega\))

Outras informações:

Coeficiente de Temperatura Passo de \(100\Omega\) Passo de \(10\Omega\) Passo de \(1\Omega\) Passo de \(0.1\Omega\)
\(\alpha_{20}\) \(~\\~(\times10^{-6}/^oC)\) \(-5~\\~+10\) \(-5~\\~+20\) \(+20~\\~+90\) \(+90~\\~+900\)
\(\beta\) \(~\\~(\times10^{-6}/^oC^2)\) \(-0.3~\\~-0.7\) \(-0.3~\\~-0.7\)
Menor Resistência para \(23^oC\) Maior Resistência para \(23^oC\) Correção Resultante Incerteza Resultante
999.978696 \(\Omega\) 1000.033587 \(\Omega\) -0.00714149999998881 \(\Omega\) \(\pm\) 0.0158456668130432 \(\Omega\)

values
\(U_{cal}\) 0.0510000
\(U_{rep}\) 0.0000000
\(U_{res mult}\) 0.2886751
\(U_{res dec}\) 0.0002887
\(U_{temp}\) 0.0158457
\(U_c\) 0.2935737
\(\nu_{eff}\) Inf
\(U_{exp}\) 0.5871480
\(C_c\) -0.0071415
1 Algarismo Significativo 2 Algarismos Significativos
RM = 0.0 \(\pm\) 0.6 \(\Omega\) com 95.45 % de confiança RM = -0.01 \(\pm\) 0.59 \(\Omega\) com 95.45 % de confiança

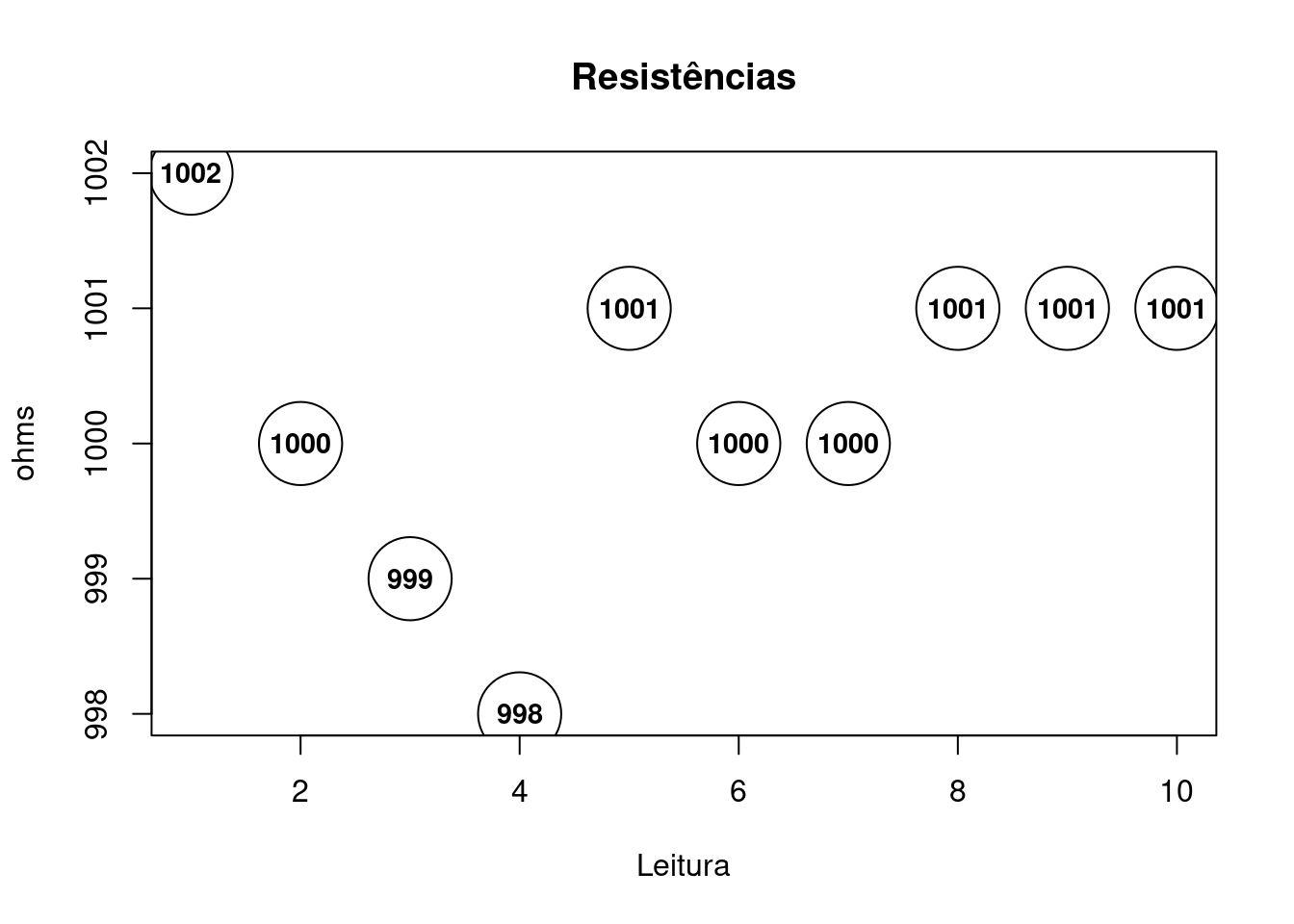
Procedimento 5: Conjunto de Resistências

Utilizando o resultado do procedimento 4 identifique o valor de uma dada resistência.

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade A Normal Amostrado
Calibração do Multímetro B Normal ver Procedimento 4
Resolução do Multímetro B Uniforme \(1\Omega\) (na escala de \(2k\Omega\))

values
\(U_{cal}\) 0.2935737
\(U_{rep}\) 1.1595018
\(U_{res}\) 0.2886751
\(U_c\) 1.2304321
\(\nu_{eff}\) 11.0000000
\(U_{exp}\) 2.7744596
\(C_c\) -0.0071415
1 Algarismo Significativo 2 Algarismos Significativos
RM = 1000 \(\pm\) 3 \(\Omega\) com 95.45 % de confiança RM = 1000.3 \(\pm\) 2.8 \(\Omega\) com 95.45 % de confiança

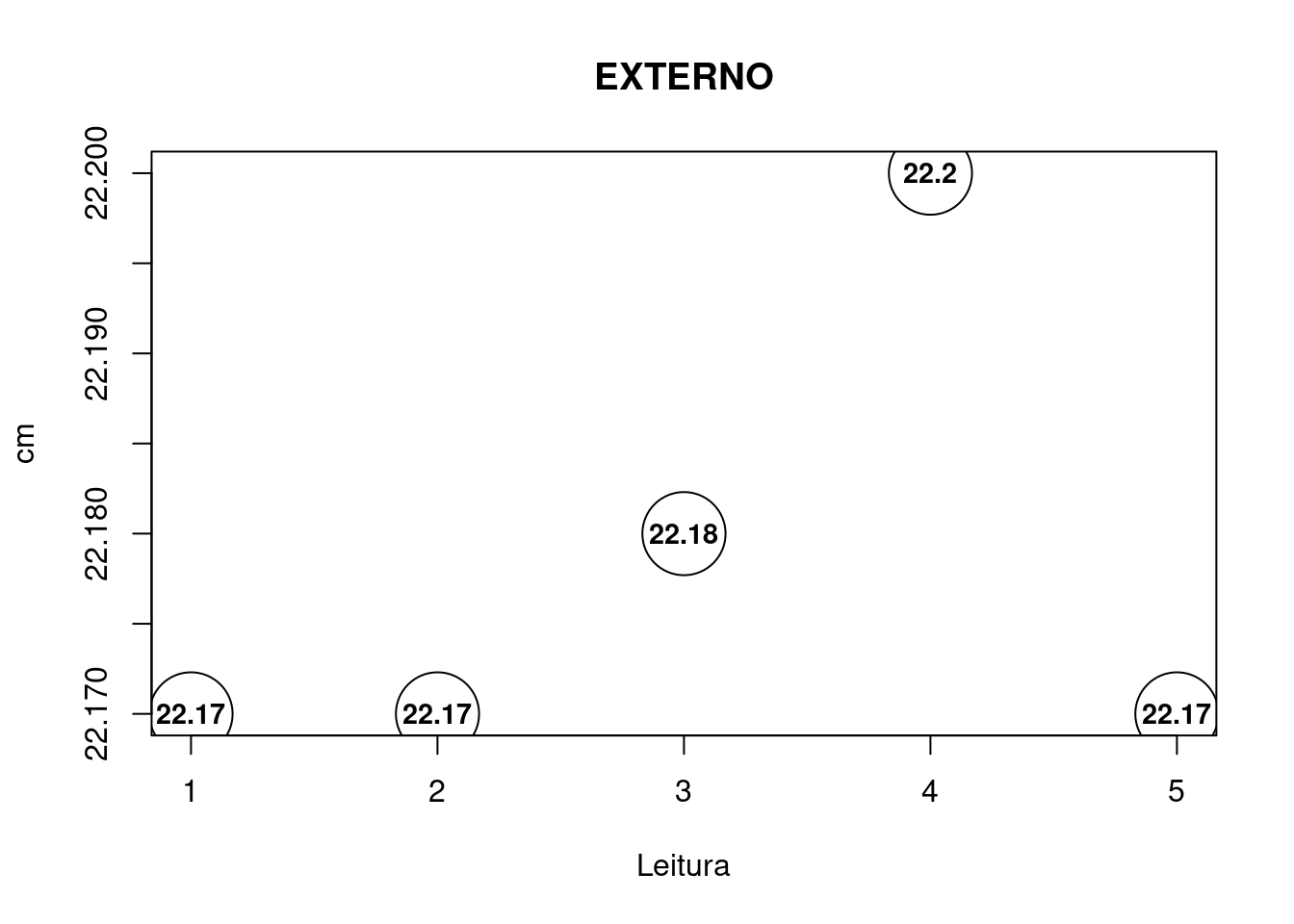
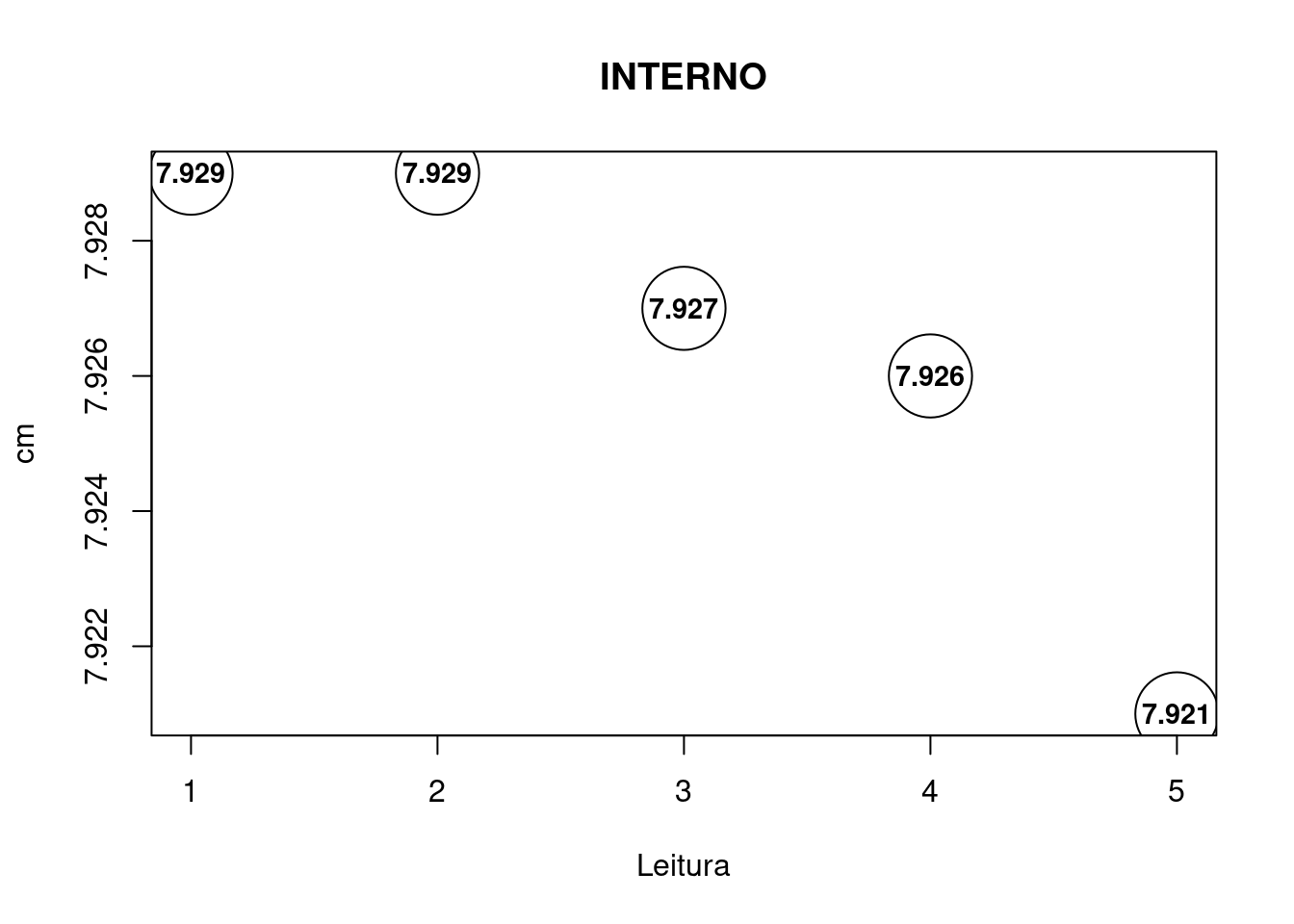
Procedimento 6: Régua e Placa de Orifício

Utilize uma régua para dimensionar \(D=D_{EXTERNO}-D_{INTERNO}\).

Modelo Matemático:

Fontes Tipos FDP Parâmetros das FDP
Repetitividade \(D_{EXTERNO}\) A Normal Amostrado
Repetitividade \(D_{INTERNO}\) A Normal Amostrado
Resolução Régua B Triangular \(0.1cm\) superior a \(10cm\) (1/3)
Resolução Régua B Triangular \(0.05cm\) até \(10cm\) (1/2)

Outras informações:

values
\(U_{rep-EXT}\) 0.0130384
\(U_{rep-INT}\) 0.0032863
\(U_{res-EXT}\) 0.0061237
\(U_{res-INT}\) 0.0051031
\(U_c\) 0.0156314
\(\nu_{eff}\) 8.0000000
\(U_{exp}\) 0.0369905
1 Algarismo Significativo 2 Algarismos Significativos
RM = 14.25 \(\pm\) 0.04 \(^oC\) com 95.45 % de confiança RM = 14.252 \(\pm\) 0.037 \(^oC\) com 95.45 % de confiança

Copyright © 2020 Guilherme Kunz, Inc. All rights reserved.