Limite Central
Desvio Padrão
Amostral
\[s^2(q_k) = \frac{1}{n-1} \sum_{j=1}^n (q_j - \overline{q})^2\]
Populacional
\[\sigma^2(q_k) = \frac{1}{n} \sum_{j=1}^n (q_j - \overline{q})^2\]
Teorema
“Quanto mais variáveis aleatórias forem combinadas, mais o comportamento da combinação resultante se aproxima do comportamento de uma distribuição normal.”
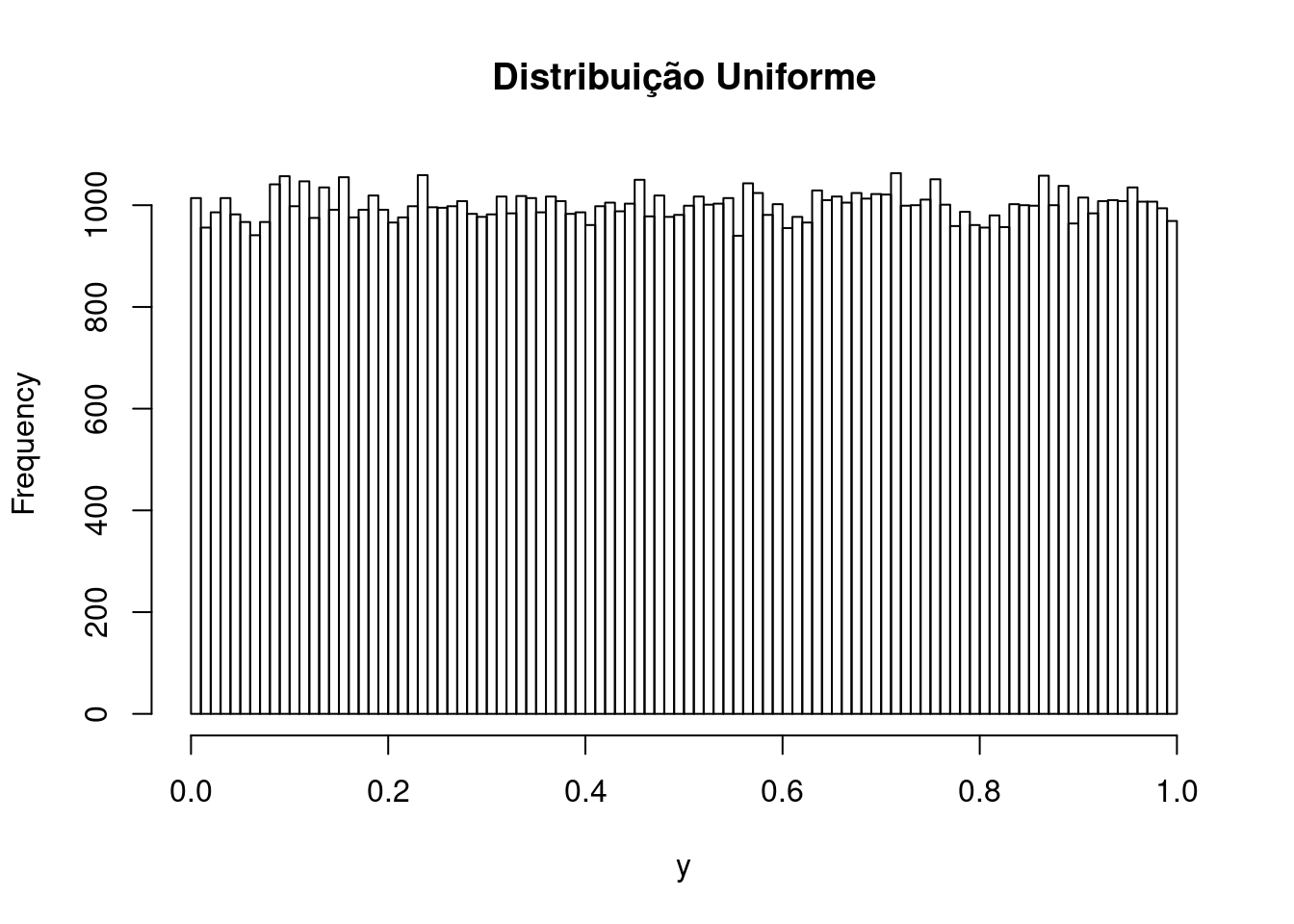
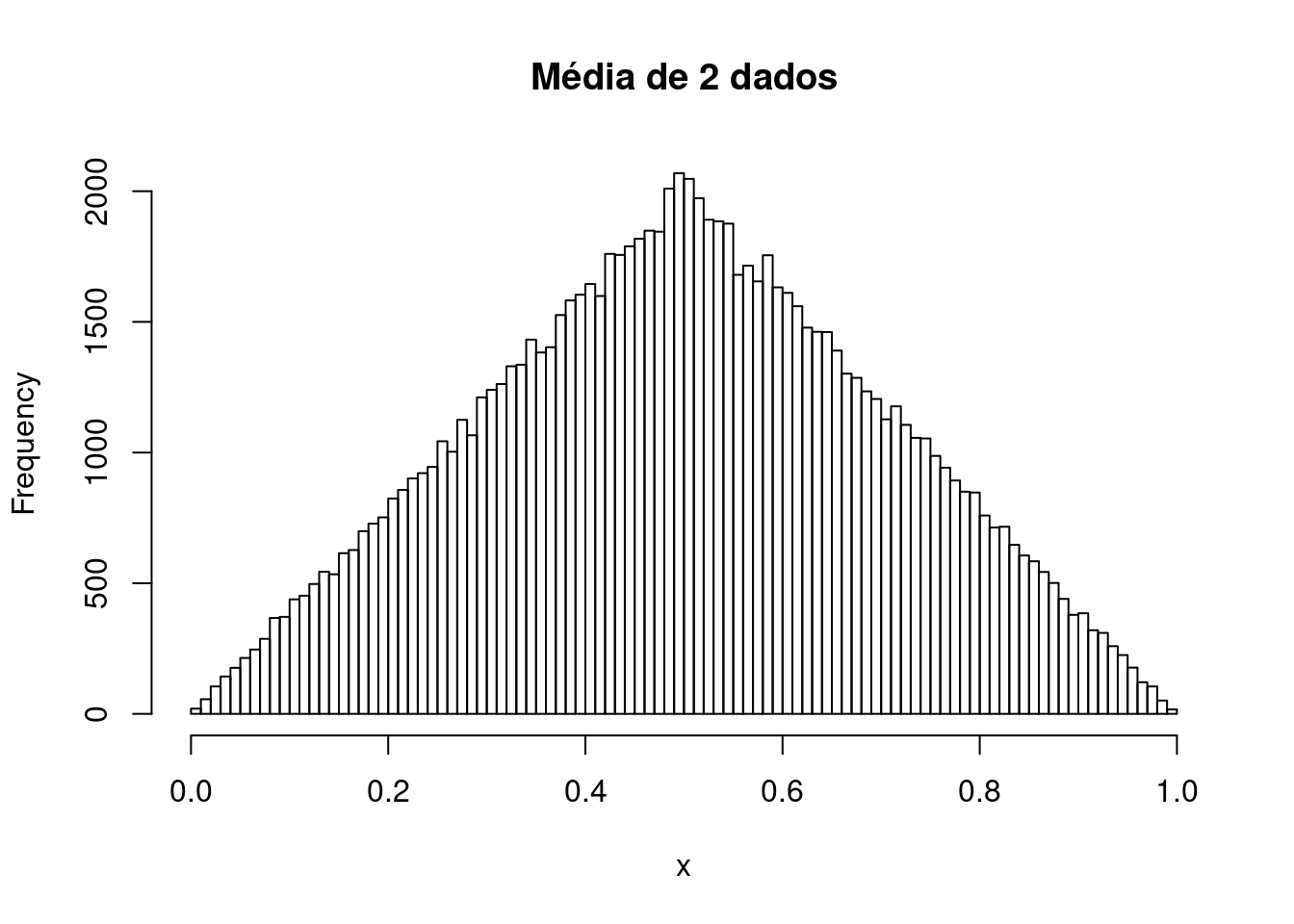
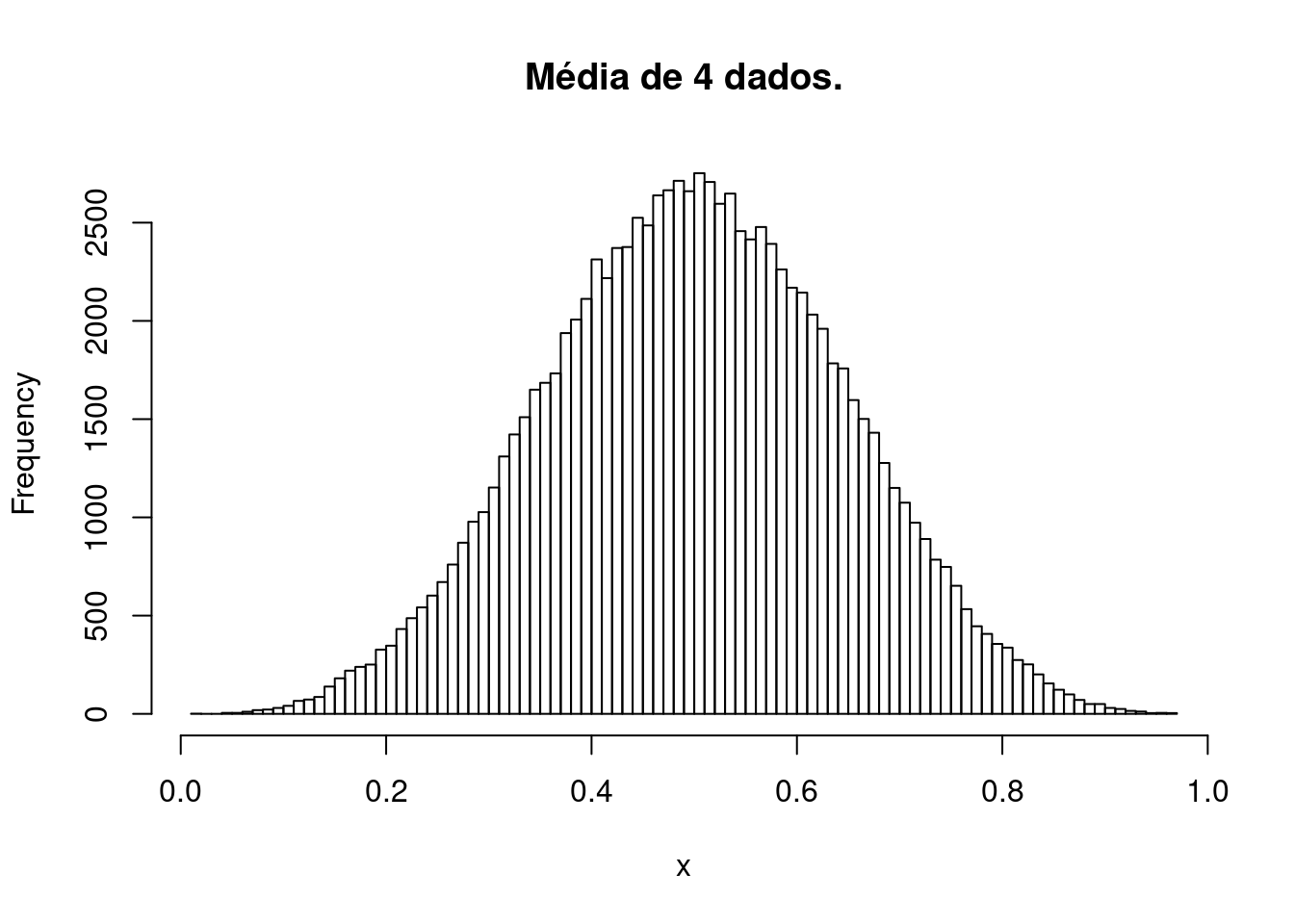
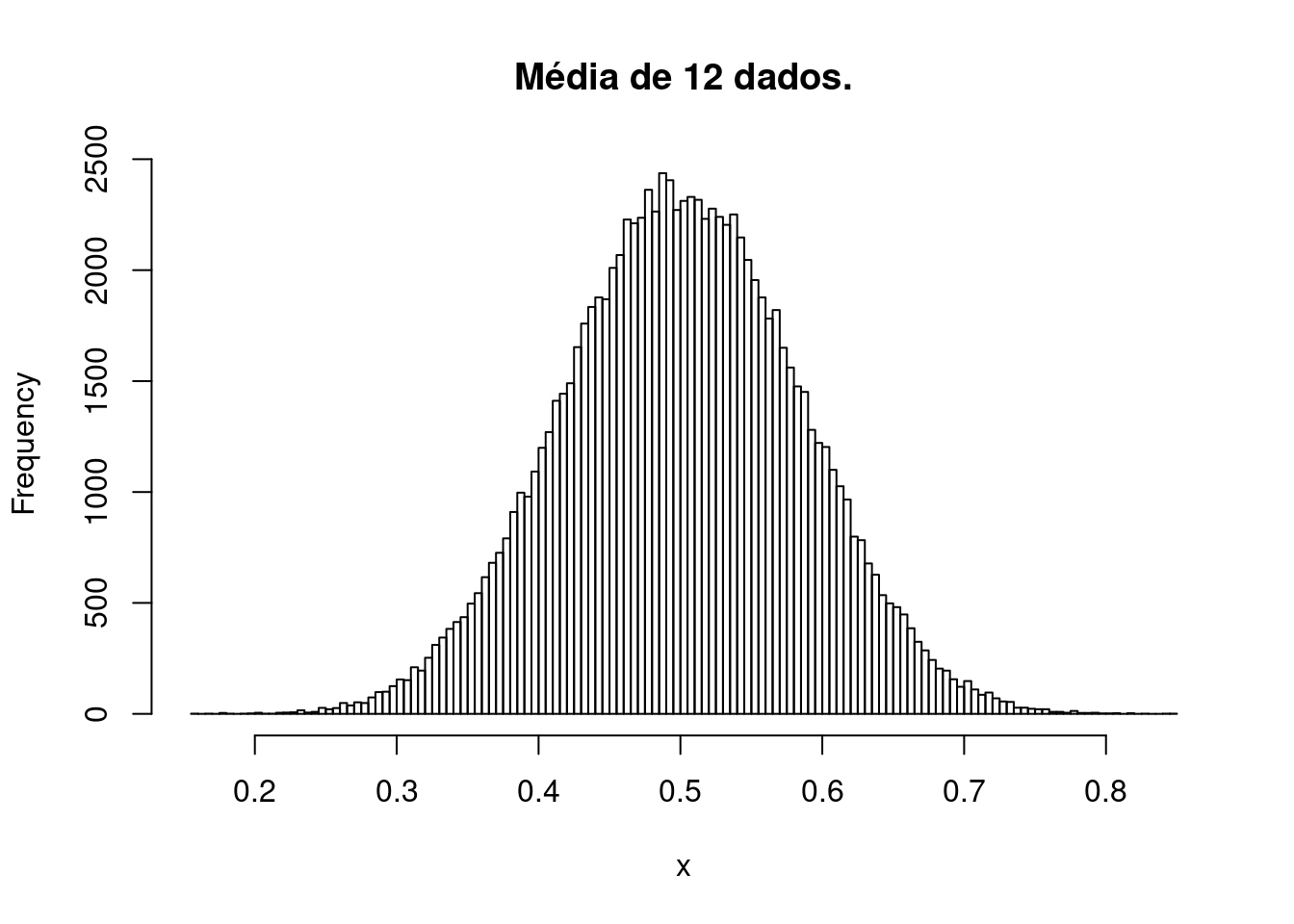
## Para estes valores aleatórios tem-se:## Para 1 s: 67.903 %
## Para 1.96 s: 95.058 %
## Para 2 s: 95.512 %
## Para 3 s: 99.803 %
## Para 4 s: 99.996 %Copyright © 2020 Guilherme Kunz, Inc. All rights reserved.